[ML] 机器学习课程 笔记本 (2) 分类
话说今天的容量好大啊。其实今天主要讲的都是分类中用到的方法,比较基础的同时也有一些比较有趣的东西,好吧开始流水账。
朴素贝叶斯 Naive Bayes
| 和开头的naive一样,这个方法几乎是可以随手想到的:利用统计的信息去进行学习并实现对未知的预测,这几乎是绝大部分人类对新事物的入门级学习方式。但是特殊的一点是,这个方法几乎是一个万能的,就是他并不一定是最好的方法,但是他至少不会太差。为什么呢,因为这个方法基于独立性假设。也就是说但凡 $$P(d | c) = P(t_1 | c)P(t_2 | c) \cdots P(t_{k} | c)dct_ikP(c)P(d | c) = P(d)P(c | d)P(c | d) \propto P(c)\prod_i{P(t_i | c)}$$。如此一来,就可以通过计算单个单词的概率,也就是贡献,来获取针对类别 C 而言的预测概率了。 |
| 那么如此一来,问题就转化成了找最大值 $$c_{\mathrm{max}} = \mathop{\mathrm{argmax}}_{c \in \mathbb{C}}\hat{P}(c | d)$$。 |
| 当然工作并没有完成,因为计算机的精度有限,小概率的乘积最后都不一定变成什么东西。所以这个时候就要取个对数了(因为取对数这个变换是保序的)。再有就是原始数据中的和$$P(t_i | c)$$很有可能出现零概率的问题,这个时候要做一个平滑处理,举例说明: |
| 平滑前 $$\displaystyle \hat{P}(t | c) = \frac{T_{ct}}{\sum_{t’ \in V}{T_{ct’}}}T_{ct}T_{ct’}$$ 为所有阳性样本中,全体单词的总数。 |
| 平滑处理后,变为计算 $$\displaystyle \hat{P}’(t | c)=\frac{T_{ct}+1}{\sum_{t’ \in V}{(T_{ct’}+1)}}=\frac{T_{ct}+1}{\sum_{t’ \in V}{T_{ct’}} + | \mathbb{V}| }|\mathbb{V}|$$ 表示单词本的容量。 |
当然直到现在依旧是纸上谈兵的东西,等我回头实现一个再说(应该很快,逃
中心向量法和 k-近邻法
讲完基于统计的方法之后,就是回到了理性分(xia)析(bai)的时候了。也就是上面的两个基于向量空间的方法,中心向量和k-近邻。
其实这两个方法真的非常简单,简单到其核心的思路就是评估待评测样本和类别之间的距离。
但是问题也随之而来,首先就是距离这个定义,用什么?欧氏距离?曼哈顿距离?还是利用夹角法?还是直接用杰卡德距离?还是选取几个方法都参考,然后写个估分?——具体问题具体分析。
其次,针对中心向量而言。中心向量其实就是选择其类别中所有样本的平均数,作为一个标杆。分别计算所有的标杆,针对每一个评测的样本,计算距离选取最近的就行了。方法确实很简单,但是对整个数据的要求近乎苛刻以至于无理。首先,数据集合必须是一个凸集。这个很显然,举一个反例就行了。比如,在做归一化处理之前,有 40 个分布在单位圆附近的一组阳性样本,还有一个模长为4000的阳性样本,一旦归一化取平均,显然这个平均点并不是我们所理想的代言人。这个时候可能你也想到了最小平方误差来确定平均。没错,我也是这样想的,但是其实没意义的。因为即便选择了最小平方误差来确定代言点,但是还是不能真正解决非凸集的问题。其二,如果数据集合是多个凸集的组合,中心向量也没用了,道理和上面论述的类似。其三,中心向量只适合解决“属于/不属于”的二义性问题,对于多模式类别,可能就真的回天乏术了。
当然,kNN 有效的解决了一部分问题。对于该算法的更一般的理解是,如果我身边最近的 5 个邻居中,有 4 个是足球球迷,那我如果提前了解一些足球知识的话,就更容易融入到社区生活当中。也就是说,对于每一个新来的样本,其身边的前 k 个近邻更利于表示其属性。当然,这个方法也有一些小问题,或者是值得思考商榷的地方。比如,k 值的选取问题,这个具体怎么样,不能凭空论断,得看训练集和测试的结果。还有训练集的大小问题,过小的训练集,和上文所讲的40个抱团一个一枝独秀是一个问题,都会严重影响结果输出(当然这个时候一般会去找数据生成的问题。。。)。再有就是距离的计算方式,欧氏距离在绝大多数情况下是够用的,但是也不能过于迷信,有的时候对于一些比较模糊的分类,比如处理音乐分类当中,如果类别只有三个:古典、摇滚、爵士,可能很多时候针对古典而言,由于其自身和摇滚也好,和爵士也好,差异太大,因为很容易区分,利用欧氏距离也很方便。但是摇滚和爵士这两个相对古典音乐而言,并不怎么容易直接利用欧氏距离来加以判断。这个时候就需要综合相似度(夹角)和距离同时考虑了。
至于算法实现,应该不难,简单写写就行了。
但是对于 kNN,注意到每一个样本过来就需要和每一个训练集的样本进行距离计算,然后再进行距离排序,效率就比较低了。如果是基于欧式距离的话,可以利用 kd-tree 加以解决。因为 kd-tree 是一个基于空间的平衡二叉树,可以将平均查询时间复杂度有效降低。如果是基于夹角计算的话,这个抱歉智力不够,不过我现在有一个非常 naive 的想法:假设原有样本是 m 维的,预处理所有的样本到一个 m 维极坐标平面上,也就是让每一个样本去和每一个轴上的单位向量计算有向角,从而得到一组 的 m+1 维向量,然后,如果要参考模长,就保留第一维,否则就直接扔掉第一维,然后剩下的就是一个简单的欧式距离就可以了,恩,闲效率不高套个 kd-tree 就行了,御坂御坂一本正经地说道!
SVM(Support Vector Machine)
我承认我的洋文不好,看到了这个名字的时候我一直念“支持向量机”,以为是“一台支持向量操作的机器”,后来才知道其实是“支持向量·机”。
你妹,支撑向量这个名字就这么不待见吗!
先不吐槽翻译,毕竟你既然学习西洋人的那一套东西,就最好直接按照西洋人的文法和习惯来称呼。如果让我强行总结这个算法的话,我可能会想到一个词:优化。
先回到前三种算法。如果成功的针对一个样例进行了分类,那么一般会考虑这个分类结果是不是线性的。为什么首先想到的是线性呢?因为线性的性质很特殊,值得研究而已。而且,相对非线性的模型,一般而言很难处理,一个折中的方法都是先线性化,然后再试着套用线性的性质。如果朴素贝叶斯和中心向量法都找到了一个非常不错的分类方法,那么就相当于,找到了分离阴阳性样本的一层硬隔板,更科学的说法是,在整个向量空间当中,找到了一个超平面,将将把这两个分割出来。其证明不写了,两个证明都很好写。但是kNN则不同,kNN准确意义上,没有给出一个硬隔板,他只是给了一个判断的方法,选取前k个就行,具体结果是什么,不得而知,很有可能如果愿意,可以画出一些非常美妙的分割图形。换言之,这个方法不是线性的。
那么如果已经找到了一个线性的分类,能不能确定这个线性分类是最好的呢?换言之,能不能接着去优化这个现有的分类,使得其更加准确呢?
思路就是这样流畅。既然是评价线性分类的好坏,那么自然要考虑,如何定义好坏一词。精确率?召回率?准确率?没错,就是从这里入手。如果有一个大法成功同时提升三者,那必然是极好的。
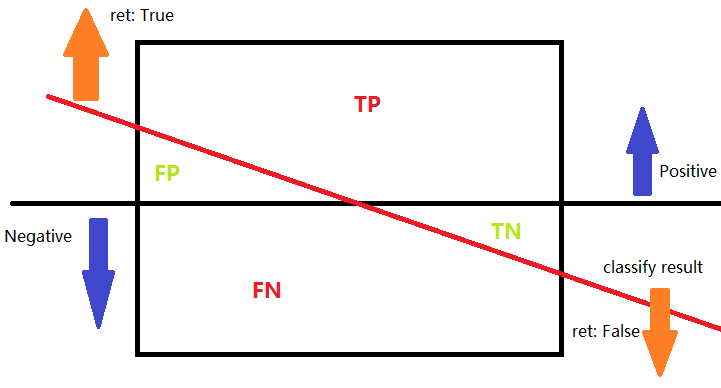
上图中的黑色实线是理论上最完美的分割方法,假设红线是目前的结果,那么最好的方法就是减少FP和TN的数量。
让我们加上数据和辅助线。
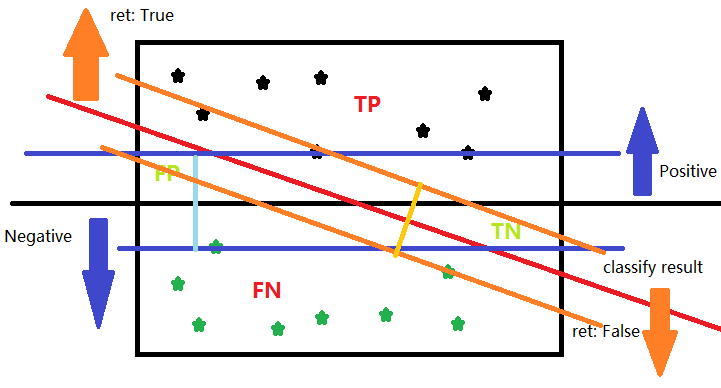
可以直观地看到,想要更准确,那就尽量保证自己的分类间隔更大。而坐落在这些分隔线上的样本如同标杆一样支撑着这个平面(二维时退化成线),因而,这些在平面上的点也叫Support Vector。所以这个问题就可以转化成一个优化问题进行求解了。
当然对于不同的小问题也有不同的策略,比如在平面上加入一个松弛项,也叫软边界。再比如将空间通过初等坐标变换,把非线性问题,转换成线性问题,再用SVM求解。
这里主要的工作就在于如何决定内积了。
决策树
谈到朴素的分类方法自然会想到因人而异这个词汇。通过审问不同的问题,可以对样本进行一种打分,然后得到最后的类别表示。当然,这里的打分的结果也不一定是一维的。
然而这个方法的问题也比较显著,比如:你这些问题怎么选择?
而且,如果选择了不错的问题,也有可能造成训练的时候表现很好,一旦来了新事物,就傻眼的情况。
你可以理解为,不会举一反三。
LLSF
今天最后讲的一个方法是基于回归分析里的一种方法,但是个人感觉更像是一个最小二乘优化。
简单讲下就是说,假设有 这样的一个类别集合,实现得知每一个训练集中的样本 ,那么可以设计一个矩阵 ,计算 ,其中表示的是每篇文章中每种特征的权值矩阵,表示的是训练集的真实情况,举个例子,已知两个类别 ,四篇文章 分别属于 ,那么可以得到
通过最小二乘法来计算出一个矩阵 ,就可以得到一个不错的分类器。
And Then What?
刚才总算把所有的今天讲的分类器写完了。。。
其实几天还讲了分类的评价和其他分类的一些小东西。。。
然而我已然已经累死了。。。
代码?不慌,让我回头写。。。